[Algorithm](EN) Swap values without temporary variable using XOR swap algorithm

Post about XOR swap algorithm

Environment and Prerequisite

• XOR
• Logic Design
• Boolean Algebra

XOR Operation

XOR

• XOR: XOR operation is bitwise operation which result 1 if they are different bit, result 0 if they are same bit.

1^1 = 0
1^0 = 1
0^1 = 1
0^0 = 0

// Example in binary
10010101
XOR
10111100

==> 00101001

// Example in decimal
149
XOR
188

==> 41

XOR Swap Algorithm

What is XOR Swap Algorithm?

• XOR Swap Algorithm is an algorithm that uses the XOR bitwise operation to swap values of distinct variables without using a temporary variable

XOR Swap Algorithm Code and Example

Example

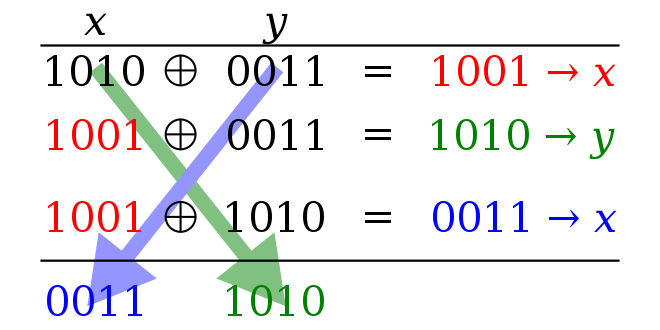
Pseudocode

X := X XOR Y
Y := Y XOR X
X := X XOR Y

C++ Code

#include <iostream>
#include <stdio.h>

using namespace std;

int main(){

    int x = 1;
    int y = 2;

    printf("x: %d y: %d\n", x, y);

    if (x != y){
        x = x^y;
        y = y^x;
        x = x^y;    
    }

    printf("x: %d y: %d\n", x, y);

    return 0;
}

Proof

Used Properties

• Commutativity: A ⊕ B = B ⊕ A
• Associativity: (A ⊕ B) ⊕ C = A ⊕ (B ⊕ C)

Proof

• Use below equation

1. X := X XOR Y
2. Y := Y XOR X
3. X := X XOR Y

R1, R2 are registers

0. R1 = X, R2 = Y

1. R1 <- R1 ⊕ R2 = X ⊕ Y
=> R1 = X ⊕ Y, R2 = Y

2. R2 <- R2 ⊕ R1 = Y ⊕ (X ⊕ Y) = Y ⊕ (Y ⊕ X) = (Y ⊕ Y) ⊕ X = 0 ⊕ X = X
=> R1 = X ⊕ Y, R2 = X

3. R1 <- R1 ⊕ R2 = X ⊕ Y ⊕ X = Y ⊕ X ⊕ X = Y ⊕ (X ⊕ X) = Y ⊕ 0 = Y
=> R1 = Y, R2 = X

Reasons for use in practice

• Embedded system of which ram memory is very limited
• In region with high register pressure

Reasons for avoidance in practice

• Due to compiler level optimization, using temporary variable is faster than XOR swap.
• It is opaque to anyone unfamiliar with the technique.
• In modern architecture, using temporary variable is faster because of instruction pipelines. Instruction pipeline enables instruction level parallel processing. XOR swap inputs to each operation depend on the results of the previous operation so it cannot be done in parallel processing.

Reference

• https://en.wikipedia.org/wiki/XOR_swap_algorithm
• https://en.wikipedia.org/wiki/Register_pressure
• https://en.wikipedia.org/wiki/Register_allocation#Spilling